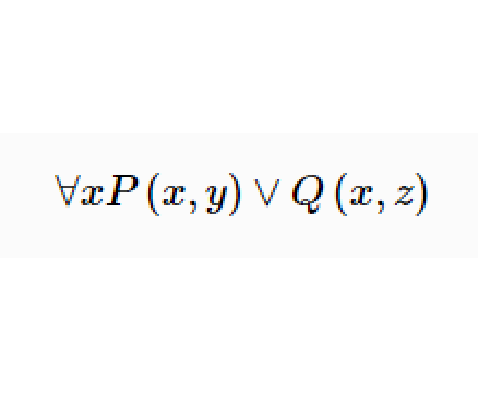合式公式是一種形式語言表達式,即形式系統中按一定規則構成的表達式。按照模型論中一種通行習慣,語言F中的合式公式定義如下:1.原子公式是合式公式; 2.若φ和ψ是合式公式,則(φ∧ψ)及(ᒣφ)是合式公式; 3.若φ是合式公式,而x是變元,則(ᗄx)φ是合式公式;4.有限次地套用1—3所得到的符號序列是合式公式。合式公式有時簡稱公式,如果一個公式φ中的自由變元都屬於集合{x1,x2,…,xe},則φ也可以記為φ(x1,x2,…,xe),不含量詞、自由變元的合式公式,分別稱為開公式和閉公式,後者又稱語句,例如R(x,y)為開公式,ᗄxR(x)是一個語句,由原子公式及聯結詞∧,∨,ᗄ,∃構成語句 稱為正語句。
基本介紹
- 中文名:合式公式
- 外文名:well-formed formula
- 簡稱:公式
- 別名:謂詞公式
- 定義:按一定規則構成的表達式
基本概念,定義,相關知識,約束變數和自由變數,合式公式的解釋,合式公式的分類,
基本概念
定義
一階邏輯中合式公式,被遞歸定義如下:
(1)原子是合式公式;
(2)若A是合式公式,則(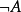 )也是合式公式;
)也是合式公式;
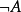
(3)若A,B是合式公式,則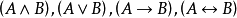 也是合式公式;
也是合式公式;
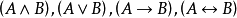
(4)若A是合式公式, 是A中的變數符號,則
是A中的變數符號,則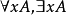 也是合式公式;
也是合式公式;

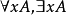
(5)只有限次地使用(1)~(4)所生成的符號串才是合式公式。
合式公式,也稱謂詞公式,簡稱為公式,為簡便起見,公式的最外層括弧可以省去。對於一個謂詞,如果其中每一個變數都在一個量詞作用之下,則它就不再是命題函式,而是一個命題了。但是,這種命題和命題邏輯中的命題還是有區別的,因為這種命題中畢竟還有變數,儘管這種變數和命題函式中的變數有所不同,因此,有必要區分這些變數。
相關知識
為了使一階邏輯中命題符號化更準確和規範,以便正確進行謂詞演算和推理,引進一階邏輯中合式公式的概念.
在形式化中,將使用以下四類符號。
(1)常量符號: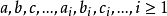 ,當論域D給出時,它可以是D中的某個元素;
,當論域D給出時,它可以是D中的某個元素;
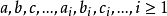
(2)變數符號: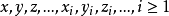 ,當論域D給出時,它可以是D中的任何一個元素;
,當論域D給出時,它可以是D中的任何一個元素;
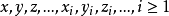
(3)函式符號:: ,當論域D給出時,n元函式符號
,當論域D給出時,n元函式符號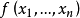 可以是
可以是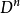 到
到 的任意一個映射;
的任意一個映射;

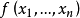
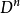

(4)謂詞符號: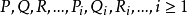 ,當論域D給出時,n元謂詞符號
,當論域D給出時,n元謂詞符號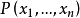 可以是
可以是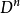 到{1,0}的任意一個謂詞。
到{1,0}的任意一個謂詞。
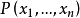
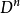
定義1一階邏輯中的項(item),被遞歸定義如下:
(1)常量符號是項;
(2)變數符號是項;
(3)若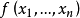 是n元函式符號,
是n元函式符號,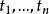 是項,則
是項,則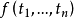 是項;
是項;
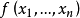
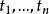
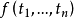
(4)只有有限次地使用(1)、(2)、(3)所生成的符號串才是項。
例如a,b,x,y是項,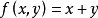 ,
, 是項,
是項,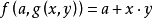 也是項。
也是項。
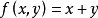

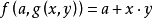
約束變數和自由變數
在一個謂詞公式中.變數的出現是約束的(bound),若且唯若它出現在使用這個變數的量詞作用範圍(稱為作用域)之內;變數的出現是自由的(free),若且唯若它的出現不是約束的;至少有一次約束出現的變數稱為約束變數(bound variable),至少有一次自由出現的變數稱為自由變數(free variable)。
例如,公式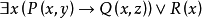 中,謂詞
中,謂詞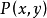 和
和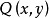 中的x的出現是約束的。而謂詞R(x)中x的出現是自由的。另外,公式中y和z的出現也是自由,因此,x既是約束變數,又是自由變數,而y,z僅僅是自由變數。由此可知,公式中的某個變數既可以是約束變數,同時也可以是自由變數。此外,顯然有
中的x的出現是約束的。而謂詞R(x)中x的出現是自由的。另外,公式中y和z的出現也是自由,因此,x既是約束變數,又是自由變數,而y,z僅僅是自由變數。由此可知,公式中的某個變數既可以是約束變數,同時也可以是自由變數。此外,顯然有
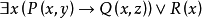
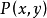
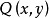


也即,一階邏輯中命題的真值,與其約束變數的記號無關。
為了避免公式中有些變數既可以約束出現,又可自由出現的情形,我們可採用以下兩條規則。
改名規則:將謂詞公式中出現的約束變數改為另一個約束變數,這種改名必須在量詞作用域內各處以及該量詞符號中進行,並且改成的新約束變數要有別於改名區域中的所有其他變數。
代替規則:對公式中某變數的所有自由出現,用另一個與原公式中的其他變數符號均不同的變數符號去代替。
例如,對於公式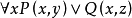 ,可使用改名規則,將約束出現的x改成u,得
,可使用改名規則,將約束出現的x改成u,得
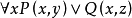
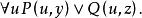
或者使用代替規則,將自由出現的x用u代替,得

這樣,對一階邏輯中的任何公式,總可以通過改名規則或代替規則,使該公式中不出現某變數既是約束變數又是自由變數的情形。
由謂詞公式的定義可知,若不對其中的常量符號、變數符號、函式符號和謂詞符號給以具體解釋,則公式是沒有實在意義的。
合式公式的解釋
定義 在一階邏輯中,公式G的一個解釋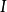 ,是由非空論域D和對G中常量符號、函式符號、謂詞符號按下列規則進行一組指定所組成:
,是由非空論域D和對G中常量符號、函式符號、謂詞符號按下列規則進行一組指定所組成:
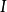
(1)對每個常量符號,指定D中的一個元素;
(2)對每個n元函式符號,指定一個函式,即指定一個 到D的映射;
到D的映射;

(3)對每個n元謂詞符號,指定一個謂詞,即指定一個 到{0,1}上的一個映射。
到{0,1}上的一個映射。

為統一起見,對所討論的公式作如下規定:公式中無自由變數,或者將自由變數看作常量。於是,每個公式在任何具體解釋下總表示一個命題。
合式公式的分類
設G是一個謂詞公式,
(1)如果存在解釋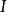 ,使
,使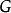 在
在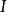 下為真(簡稱
下為真(簡稱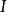 滿足
滿足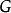 ),則稱
),則稱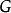 是可滿足的;
是可滿足的;
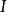
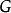
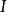
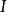
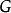
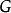
(2)如果所有解釋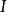 均不滿足
均不滿足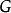 ,(簡稱
,(簡稱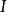 弄假
弄假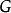 ),則稱
),則稱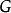 為恆假的,或不可滿足的;
為恆假的,或不可滿足的;
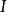
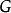
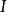
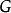
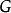
(3)如果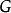 的所有解釋
的所有解釋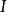 都滿足
都滿足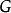 ,則稱
,則稱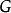 為恆真的。
為恆真的。
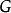
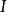
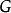
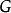
如果一階邏輯中的恆真(恆假)公式,要求所有解釋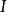 均滿足(弄假)該公式,而解釋
均滿足(弄假)該公式,而解釋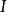 依賴一個非空個體集合D,又集合D可以是無窮集合,而集合D的“數目”也可以有無窮多個,因此,所謂公式的“所有”解釋,實際上是很難考慮的,這就使得一階邏輯中公式的恆真、恆假性的判定異常困難。Church和Turing分別於1936年獨立地證明了:對於一階邏輯,判定問題是不可解的,即不存在一個統一的算法A,該算法與謂詞公式無關,使得對一階邏輯中的任何謂詞公式G,A能夠在有限步內判定公式G的類型。
依賴一個非空個體集合D,又集合D可以是無窮集合,而集合D的“數目”也可以有無窮多個,因此,所謂公式的“所有”解釋,實際上是很難考慮的,這就使得一階邏輯中公式的恆真、恆假性的判定異常困難。Church和Turing分別於1936年獨立地證明了:對於一階邏輯,判定問題是不可解的,即不存在一個統一的算法A,該算法與謂詞公式無關,使得對一階邏輯中的任何謂詞公式G,A能夠在有限步內判定公式G的類型。
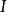
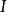
但是,一階邏輯是半可判定的,即如果謂詞公式G是恆真的,有算法在有限步內檢驗出G的恆真性。