傳遞集是一種特殊的集合，主要用於數學領域。在關係“～”下 Ω 點每個等價類，稱為 G 點一個軌道或傳遞集。而 Ω 是 G 的一些軌道的無交並。如果 Ω 本身是 G 的一個軌道，就說 G 是 Ω 上的傳遞群（transitive group）。
基本介紹
- 中文名：傳遞集
- 外文名：transitive set
- 適用範圍：數理科學
簡介,傳遞性,
簡介
設 G 為Ω 上的置換群。藉助 G 可以在Ω 上定義一種關係：點α 與β 有關係“～”，或α～β，如果有 G 中元素 g 使
。顯然關係”～”有反身性，對稱性和傳遞性，即“～”是一個等價關係。在此關係“～”下 Ω 點每個等價類，稱為 G 點一個軌道（orbit）或傳遞集。而 Ω 是 G 的一些軌道的無交並。如果 Ω 本身是 G 的一個軌道，就說 G 是 Ω 上的傳遞群（transitive group）。
傳遞性
[transitivity]
設 G 為Ω 上的置換群，
。G 的全體以α 為不動點的元素組成一個子群，稱為α 在 G 內的穩定子群（stabilizer），記作
。設
為 G 在Ω 上的一個軌道，而且
。此時若β 也為 中一點，那么，G 中把α 映成β 的那些元素組成的集合正好也是 在 G 內的一個右陪集。反過來， 在 G 內的任何一個右陪集的各元素都把α 映成 中的同一個點。因此在點集合 和 點右陪集所成的集合間右一個一一對應。於是， 點長度正好是 在 G 內的指數。於是得到公式
。當 G 在Ω 上傳遞時，有
。由此知道，傳遞群 G 的階一定是Ω 的長度的倍數。若α，β點點屬於 G 的同一軌道 ，則它們的穩定子群在 G 內共軛。
前述點點穩定子群的概念可推廣到子集上。設 是Ω 的子集。G 中把 作為集合還變成 的全體元素組成一個子群，稱為 在 G 中的集型穩定子群（set-wise stabilizer）。而 G 中把 里每個點都保持不變的元素組成子群稱為 在 G 中的點型穩定子群（point-wise stabilizer）。當
時，我們把 當集型穩定子群記作
。而把 的點型穩定子群記作
。
仍設 G 為Ω 上點置換群。用Ω（k）表示Ω 的 k 元有序子集組成的集合。每個群元素
都引起Ωk的一個置換：
。於是 G 作用於集合Ωk上。把 G 看成Ωk上的置換群，如果是傳遞群，則說 G 在Ω 是 k 重傳遞的（k-transitive）。一個等價的說法是：群 G 在Ω 是 k 重傳遞的，如果對 Ω 的任意的 k 個不同的點
和任意的 k 個不同的點
，G 中都有一個元素 g 使得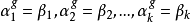
同時成立。由此知前面所說的 G 在Ω 上傳遞實際上就是 G 在Ω 上是1重傳遞的。2重傳遞群也稱雙傳遞群。習慣上當k>1時，k重傳遞群稱為多重傳遞群。k>1時Ω 上的 k 重傳遞群也是
重傳遞群。若 G 是Ω 上的 k 重傳遞群，則 G 的階是
的倍數，這裡 n 為Ω 的長度。若
，則Sym（Ω）是Ω 上的 n 重傳遞群。而當
時，Alt（Ω）是Ω 上的
重傳遞群。
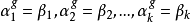
對多重傳遞群的研究從來是置換群理論的最重要的課題。背景是，雖然當
時，存在無窮多個 k 重傳遞群，但是，除去對稱群和交錯群外，人們只知道四個4重傳遞群，即馬蒂厄群
和
,這裡
和 是5重傳遞群。在有限單群分類定理獲證之後，人們才知道確實不存在其他的4重和5重傳遞群。利用單群分類定理，人們已經可以不遺漏地羅列出所有的2重傳遞群。
