基本介紹
- 中文名:保序映射
- 外文名:order-preserving mapping
- 性質:序論中的一種重要映射
- 所屬學科:數學
- 相關概念:偏序集,反序映射等
基本介紹






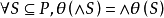












相關定理




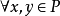










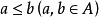












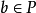


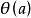


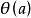


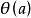


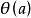







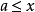














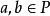



格的保序映射



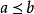
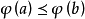













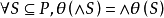
















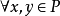










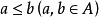












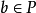


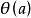


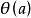


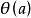


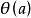







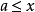














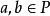






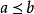
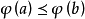






保序映射(order-preserving mapping)是序論中的一種重要映射,設f:P→Q是偏序集P到偏序集Q的映射,對任意a,b∈P,若a≤b有f(a)≤f(b) (f(a)≥f(b))...
因此,可以定義一個從序數全域到所有無窮良序基數構成的真類上的保序映射,使得ᗄα<β((α)<(β)),式中讀做“阿列夫”。還常用Nα代替(α),表示第α個...
因此,可以定義一個從序數全域到所有無窮良序基數構成的真類上的保序映射,使得ᗄα<β((α)<(β)),式中讀做“阿列夫”。還常用α代替(α),表示第α個無窮...
成為一個序集,那么 A 中抽取 m 個元素的一個組合對應於數段 到序集 A 的一個確定的嚴格保序映射。組合數 的常用符號還有組合數性質 編輯 互補...
如果給集A編序 成為一個序集,那么A中抽取m個元素的一個組合對應於數段 到序集A的一個確定的嚴格保序映射,組合數 的常用符號還有 [1] ...
編撰出版了《保序映射與積分過程》、《隨機微積分與隨機模型》等多種專著。詞條標籤: 科學家 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:6次歷史版本 最近...
因此,可以定義一個從序數全域到所有無窮良序基數構成的真類上的保序映射 ,使得ᗄα<β( (α)< (β)),式中讀做“阿列夫”。還常用 α代替(α),表示第α...
1.2.2保序映射.剩餘映射與序同構1.2.3格及其理想(濾子)1.3布爾代數及其各種推廣1.3.1布爾代數、Ockham代數與DeMorgan代數1.3.2偽補與Heyting格(代數)...
因此,可以定義一個從序數全域到所有無窮良序基數構成的真類上的保序映射,使得ᗄα<β( (α)< (β)),式中 讀做“阿列夫”。還常用 α代替 (α),表示第...
13. 基於保序映射的決策形式背景的屬性約簡 .researchgate.2012-4-15[引用日期2016-10-31] 14. 形式背景中的粒計算與知識約簡 .道客巴巴.2009-4-15[引用...
《現代數學基礎43:格論導引》講述格論的基本概念與基礎知識。其內容涵蓋:有序集、保序映射、格與半格、完全格、理想與同態、格同餘等基本概念;模格與半模格;...
7.2 嚴格保序映射下的DEA有效性分析7.3 套用偏序集理論研究數據變換的不變性7.4 基於偏序集理論的DEA方法7.5 P-DEA方法在一類數據離散型評價問題中的套用...
度結構的自同構(automorphism of degrees'structure)遞歸論的基本概念之一指度結構到其自身的一一保序映射.若f為羅~少的一一映射,且對任何x,yE},x<yHf(x)<f...
3.2.3保序變換奇異值分解(OPT-SVD)算法的過程描述3.3保序變換算法在基因組序列相似度/相異度分析中的套用3.4本章結論第4章基於保距映射算法的基因組序列Map...
