五次曲線:簡介,在歐幾里得幾何中,非平面代數曲線,代數函式域,理性曲線,

在數學中，平面實數代數曲線是歐幾里得平面上的坐標集合，其坐標是兩個變數中的一些多項式的零點。更一般來說，代數曲線是相似的，但是可以嵌入在較高維度空間中或者在一些更通用的場上被定義。

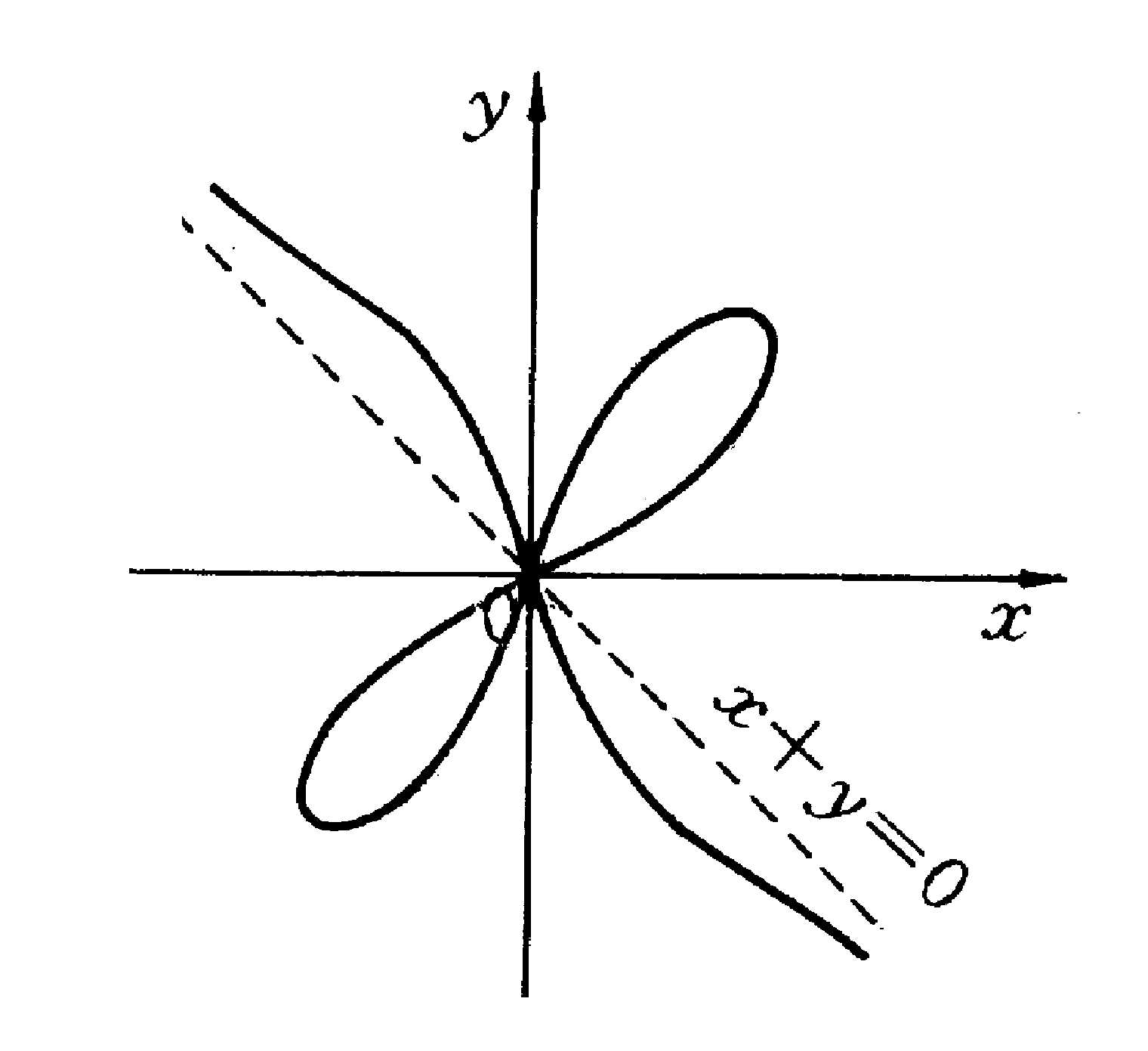
五次曲線(quintic curve)是數學中一種常見的曲線。即在平面仿射坐標系(包括直角坐標系)中，五次方程表示的曲線。例如，五次方程x^5-2x^2y+y^5=0表示圖中的曲線。

基本介紹

中文名：五次曲線
外文名：quintic curve
領域：代數幾何
特徵：自變數最高次為5次
定義：五次方程表示的曲線
示例：x^5-2x^2y+y^5＝0
別名：代數曲線

簡介,在歐幾里得幾何中,非平面代數曲線,代數函式域,理性曲線,

簡介

例如，單位圓是一個實數代數曲線，是多項式x² + y²=1的點的集合。

各種技術考慮導致多項式的複雜零被認為屬於曲線。此外，代數曲線的概念已經被推廣，以允許定義多項式的係數和曲線的點的坐標屬於任何場，導致以下定義。

在代數幾何中，在域k上定義的平面仿射代數曲線是K²的坐標集合，其坐標是具有k係數的一些雙變數多項式的零點，其中K是k的一些代數閉合擴展。坐標為k的曲線的點是曲線的k點，並且是曲線的k部分。

例如，（2，√-3）是由x² + y² - 1 = 0定義的曲線點，通常的單位圓是該曲線的實部。術語“單位圓”可以指所有的複雜點，也可以指實際點，從上下文中通常清楚的確切含義。方程式x² + y² + 1 = 0定義了一個代數曲線，其實部為空。

更一般地，可以考慮不包含在平面中但在更高維度的空間中的代數曲線。不包含在某個平面中的曲線稱為偏斜曲線。扭曲代數曲線的最簡單的例子是扭曲的立方體。人們還可以考慮投影空間中包含的代數曲線，以及與在仿射或投影空間中嵌入的獨立定義的代數曲線。這導致代數曲線的最一般定義：

在代數幾何中，代數曲線是維度一的代數變數。

在歐幾里得幾何中

歐幾里德平面中的代數曲線是其坐標是雙變數多項式方程p（x，y）= 0的解的點集合。該方程通常稱為曲線的隱式方程，通過與曲線相反的曲線是明確定義y作為x的函式的函式的圖形。

使用這樣一個隱式方程給出的曲線，第一個問題是確定曲線的形狀並繪製曲線。這些問題並不像在功能圖中的情況那樣容易解決，對於這種函式，可以容易地為x的各種值計算y。定義方程是一個多項式的事實意味著曲線具有一些可能有助於解決這些問題的結構性質。

每個代數曲線可以被唯一地分解成有限數量的平滑單調弧（也稱為分支），通過有時被稱為“顯著點”的某些點連線。平滑單調弧是在x軸的開放間隔上定義和單調的平滑函式的曲線圖。在每個方向上，弧線是無界的（通常稱為無限弧），或者具有一個終點，它是一個奇異點（這將在下面定義）或一個切線平行於一個坐標軸的點。

例如，對於圖的Tschirnhausen立方，有兩個無限弧，其原點（0,0）為終點。這一點是曲線的唯一奇點。有兩個弧具有這個奇異點作為一個端點並且具有水平切線的第二終點。最後，還有另外兩個弧，其中這些點具有水平切線作為第一個終點，並且將具有垂直切線的唯一點與第二個終點共享。另一方面，正弦曲線肯定不是代數曲線，具有無限數量的單調弧。

要繪製一個代數曲線，重要的是要知道它們的顯著點和切線，無限分支及其漸近線（如果有的話）以及圓弧連線它們的方式。也可以將拐點考慮在內。當所有這些信息在紙張上繪製時，曲線的形狀通常相當清楚。如果不是，可以添加其他幾個點和它們的切線，以獲得曲線的良好描述。

非平面代數曲線

代數曲線是維度一的代數變數。這意味著維數n的仿射空間中的仿射曲線由n個變數中的至少n-1個多項式定義。為了定義一個曲線，這些多項式必須產生Krull維1的主要理想。這種情況在實踐中不容易測試。因此，可以以下列方式來表示非平面曲線。

讓

是兩個變數x1和x2中的n個多項式，使得f是不可約的。維度n的仿射空間中的點，其坐標滿足方程和不等式：

是有限數量的點被刪除的代數曲線的所有點。該曲線由多項式h的理想的發生器系統定義，使得其存在整數kk使得

屬於由

。該表示是由f定義的曲線和平面曲線之間的有理等價。每個代數曲線都可以這樣表示。然而，可能需要變數的線性變化，以使得幾乎總是將投影注入到兩個第一變數上。當需要改變變數時，幾乎每一個變化都是方便的，一旦它被定義在一個無限的領域。

該表示允許我們從其平面投影的相應屬性容易地推導出非平面代數曲線的任何屬性，包括其圖形表示。

對於由其隱式方程定義的曲線，曲線的上述表示可以從Gröbner基礎中輕易地推導出塊排序，使得較小變數的塊為（x1，x2）。多項式f是基數中唯一依賴x1和x2的唯一多項式。通過選擇i = 3，...，n，在xi中為線性的多項式，並且僅依賴於x1，x2和xi來獲得分數gi / g0。如果這些選擇是不可能的，這意味著方程式定義一個不是多樣性的代數集合，或者該種類不是維度一，或者必須改變坐標。後一種情況發生在f存在且唯一的情況下，並且對於i = 3，...，n，存在多項式，其前導單項只取決於x1，x2和xi。

代數函式域

代數曲線的研究可以減少到不可約代數曲線的研究：不能寫成兩個較小曲線的並集的曲線。直到雙等效，欄位F上的不可約曲線分別等價於F上的一個變數中的代數函式欄位。這樣的代數函式欄位是F的欄位擴展K，其包含超過F的元素x， K是F（x）的有限代數擴展，它是不確定x在F上的理性函式的領域。

例如，考慮複數的欄位C，我們可以在C中定義C中的有理函式的欄位C（x）。如果y² = x³-x-1，則欄位C（x，y）是橢圓函式領域。元素x不是唯一確定的;該場也可以被認為是例如C（y）的擴展。對應於函式域的代數曲線只是C2中滿足y² = x³-x-1的點（x，y）集合。

如果欄位F不是代數關閉的，那么函式欄位的觀點比考慮點的軌跡更加一般，因為我們包括例如沒有點的“曲線”。例如，如果基欄位F是實數的欄位R，則x² + y² = -1定義了R（x）的代數擴展欄位，但是被認為是R2的子集的相應曲線沒有點。方程式x² + y² = -1在方案意義上（R中有限類型的積分，分離的一維方案）定義了R上的不可約代數曲線。在這個意義上，在F之間的不可約代數曲線（直到雙等效）和一個變數中的代數函式域之間的一對一對應關係一般。

兩條曲線可以是雙等效的（即具有同構函式域），而不是同構的曲線。當處理非奇異曲線時，情況變得更加容易，即那些缺乏奇點的曲線。若且唯若它們的函式域是同構的時，場上的兩個非奇異投影曲線是同構的。

特森定理是關於代數閉合場上的代數曲線的函式域。

理性曲線

一個合理的曲線，也稱為單軌曲線，是任意一條曲線，它們與一條線相當，它們可能是一條投影線；因此，我們可以在一個不確定的F（x）中用理性函式的場來識別曲線的函式域。如果F代數閉合，這相當於零類曲線;然而，在真實代數變數x² + y² = -1上定義的所有實數代數函式的領域是不屬於理性函式域的零屬性的領域。

具體來說，通過以單個參數t定義的n個有理函式，可以將尺寸n超過F的合理曲線參數化（除了孤立的異常點）;通過清除分母，我們可以將其轉化為投影空間中的n + 1個多項式函式。一個例子就是理性的正態曲線。

在F上定義的任何錐形截面是F的合理點，是一個合理的曲線。通過合理點繪製具有斜率t的線，並與平面二次曲線交點進行參數化;這給出了具有F-有理係數和一個F-有理根的多項式，因此另一個根也是F-合理（即屬於F）。

2+xy+y²=1" style="float: right;" picsrc="e61190ef76c6a7ef8865a1e8f7faaf51f2de66b8" data-layout="right" width="220" height="220" url="https://gss2.bdstatic.com/-fo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=93478afe30f33a879a6d0718f65d1018/e61190ef76c6a7ef8865a1e8f7faaf51f2de66b8.jpg" compressw="220" compressh="220" useredit="1" />例如，考慮橢圓x² + xy + y² = 1，其中（-1,0）是一個有理點。用（-1,0），y = t（x + 1）的斜率t繪製一條線，在橢圓方程中代入，求解x，得到：

x<sup class=