二階導數

二階導數，是原函式導數的導數，將原函式進行二次求導。一般的，函式y=f（x）的導數y‘=f’（x）仍然是x的函式，則y’=f’（x）的導數叫做函式y=f（x）的二階導數。在圖形上，它主要表現函式的凹凸性。

基本介紹

• 中文名：二階導數
• 外文名：the second derivative test
• 含義：原函式導數的導數
• 幾何意義1：切線斜率變化的速度
• 幾何意義2：函式的凹凸性
• 標記方式：y''=d^2y/dx^2即y=（y）
• 套用：判斷函式凹凸等
• 套用科學：數學

代數記法

二階導數記作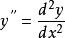即y''=（y'）'。

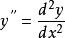
例如：y=x²的導數為y'=2x，二階導數即y'=2x的導數為y''=2。

幾何意義

（1）切線斜率變化的速度，表示的是一階導數的變化率。

（2）函式的凹凸性（例如加速度的方向總是指向軌跡曲線凹的一側）。

這裡以物理學中的瞬時加速度為例:

根據定義有

可如果加速度並不是恆定的，某點的加速度表達式就為：

a=limΔt→0 Δv/Δt=dv/dt(即速度對時間的一階導數)

又因為v=dx/dt 所以就有：

a=dv/dt=d²x/dt² 即元位移對時間的二階導數

將這種思想套用到函式中 即是數學所謂的二階導數

f'(x)=dy/dx (f(x)的一階導數）

f''(x)=d²y/dx²=d(dy/dx)/dx (f(x)的二階導數)

對於反函式

設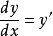,則，應視為y的函式

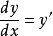
則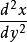

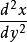
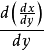=（定義）

=

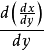
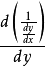
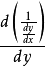
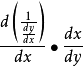=（複合函式求導，x是中間變數）

=

=

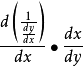
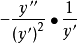
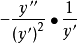
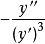
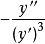
所以，反函式的二階導數不是原函式二階導數的倒數。

性質

（1）如果一個函式f(x)在某個區間I上有f''(x)（即二階導數）>0恆成立，那么對於區間I上的任意x,y，總有：

f(x)+f(y)≥2f[(x+y)/2]，如果總有f''(x)<0成立，那么上式的不等號反向。

幾何的直觀解釋：如果一個函式f(x)在某個區間I上有f''(x)（即二階導數）>0恆成立，那么在區間I上f(x)的圖象上的任意兩點連出的一條線段，這兩點之間的函式圖象都在該線段的下方，反之在該線段的上方。

（2）判斷函式極大值以及極小值。

結合一階、二階導數可以求函式的極值。當一階導數等於0，而二階導數大於0時，為極小值點。當一階導數等於0，而二階導數小於0時，為極大值點；當一階導數和二階導數都等於0時，為駐點。

（3）函式凹凸性。

設f(x)在[a,b]上連續，在（a,b)內具有一階和二階導數，那么，

（1）若在（a,b)內f''(x)>0,則f(x)在[a,b]上的圖形是凹的；

（2）若在（a,b)內f’‘(x)<0,則f(x)在[a,b]上的圖形是凸的。