二叉樹遍歷

所謂遍歷(Traversal)是指沿著某條搜尋路線，依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴於具體的套用問 題。 遍歷是二叉樹上最重要的運算之一，是二叉樹上進行其它運算之基礎。

基本介紹

• 中文名：二叉樹遍歷
• 外文名：Binary Tree Traversal
• 一棵非空的二：由根結點及左、右子樹這三個基本
• 叉樹：部分組成
• 在任一給定結：可以按某種次序執行三個操作

算法實現

遍歷方案

從二叉樹的遞歸定義可知，一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此，在任一給定結點上，可以按某種次序執行三個操作：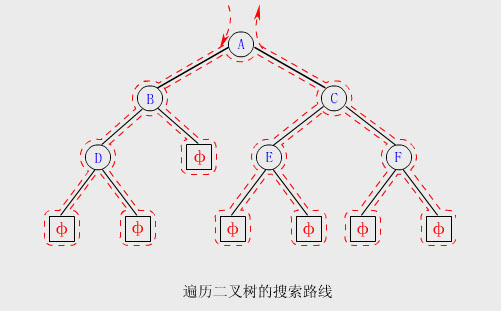

二叉樹的前序遍歷

⑴訪問結點本身（N），

⑵遍歷該結點的左子樹（L），

⑶遍歷該結點的右子樹（R）。

以上三種操作有六種執行次序：

NLR、LNR、LRN、NRL、RNL、RLN。

注意：

前三種次序與後三種次序對稱，故只討論先左後右的前三種次序。

遍曆命名

根據訪問結點操作發生位置命名：

① NLR：前序遍歷(Preorder Traversal 亦稱（先序遍歷））

——訪問根結點的操作發生在遍歷其左右子樹之前。

② LNR：中序遍歷(Inorder Traversal)

——訪問根結點的操作發生在遍歷其左右子樹之中（間）。

③ LRN：後序遍歷(Postorder Traversal)

——訪問根結點的操作發生在遍歷其左右子樹之後。

注意：

由於被訪問的結點必是某子樹的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和後根遍歷。

遍歷算法

1．先（根）序遍歷的遞歸算法定義：

若二叉樹非空，則依次執行如下操作：

⑴ 訪問根結點；

⑵ 遍歷左子樹；

⑶ 遍歷右子樹。

2．中（根）序遍歷的遞歸算法定義：

若二叉樹非空，則依次執行如下操作：

⑴遍歷左子樹；

⑵訪問根結點；

⑶遍歷右子樹。

3．後（根）序遍歷得遞歸算法定義：

若二叉樹非空，則依次執行如下操作：

⑴遍歷左子樹；

⑵遍歷右子樹；

⑶訪問根結點。

中序算法實現

用二叉鍊表做為存儲結構，中序遍歷算法可描述為：

void InOrder(BinTree T)

{ //算法里①~⑥是為了說明執行過程加入的標號

① if(T) { // 如果二叉樹非空

② InOrder(T->lchild）；

③ printf("%c"，T->data）； // 訪問結點

④ InOrder(T->rchild);

⑤ }

⑥ } // InOrder

中序投影法

計算中序遍歷擁有比較簡單直觀的投影法，如圖

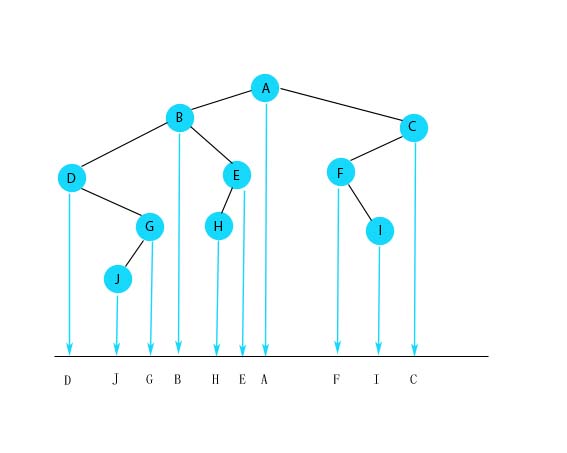中序遍歷的投影法

層序遍歷

除了先序遍歷、中序遍歷、後序遍歷外，還可以對二叉樹進行層序遍歷。設二叉樹的根節點所在層數為1，層序遍歷就是從所在二叉樹的根節點出發，首先訪問第一層的樹根節點，然後從左到右訪問第2層上的節點，接著是第三層的節點，以此類推，自上而下，自左至右逐層訪問樹的結點的過程就是層序遍歷。

遞歸實現

在這裡，所有的二叉樹都以數組的形式儲存。

前序遍歷

procedure first(i:longint);beginwrite(a[i]);ifa[i*2]<>0then first(i*2）；ifa[i*2+1]<>0then first(i*2+1）；end;

中序遍歷

procedure mid(i:longint);beginif a[i*2]<>0 then mid(i*2）；write(a[i]);if a[i*2+1]<>0 then mid(i*2+1）；end;

後序遍歷

procedure last(i:longint);beginif a[i*2]<>0 then last(i*2）；if a[i*2+1]<>0 then last(i*2+1）；write(a[i]);end;

注意事項

⑴在搜尋路線中，若訪問結點均是第一次經過結點時進行的，則是前序遍歷；若訪問結點均是在第二次（或第三次）經過結點時進行的，則是中序遍歷（或後序遍歷）。只要將搜尋路線上所有在第一次、第二次和第三次經過的結點分別列表，即可分別得到該二叉樹的前序序列、中序序列和後序序列。

⑵上述三種序列都是線性序列，有且僅有一個開始結點和一個終端結點，其餘結點都有且僅有一個前驅結點和一個後繼結點。為了區別於樹形結構中前驅（即雙親）結點和後繼（即孩子）結點的概念，對上述三種線性序列，要在某結點的前驅和後繼之前冠以其遍歷次序名稱。

【例】上圖所示的二叉樹中結點C，其前序前驅結點是D，前序後繼結點是E；中序前驅結點是E，中序後繼結點是F；後序前驅結點是F，後序後繼結點是A。但是就該樹的邏輯結構而言，C的前驅結點是A，後繼結點是E和F。

二叉鍊表基本思想

基於先序遍歷的構造，即以二叉樹的先序序列為輸入構造。

注意：

先序序列中必須加入虛結點以示空指針的位置。

【例】

建立上圖所示二叉樹，其輸入的先序序列是：ABD∮∮∮CE∮∮F∮∮。

構造算法

假設虛結點輸入時以空格字元表示，相應的構造算法為：

// 二叉樹的創建一般都是通過遞歸的方式創建void CreateBinTree(BinTree **T) {    //構造二叉鍊表。T是指向根指針的指針，故修改*T就修改了實參（根指針）本身     char ch;    if ( (ch = getchar()) == ' ' ) {        *T = NULL; //讀入空格，將相應指針置空    } else { //讀人非空格         *T = (BinTNode * ) malloc(sizeof(BinTNode)); //生成結點         (*T)->data = ch;        CreateBinTree( &(*T)->lchild ); //構造左子樹         CreateBinTree( &(*T)->rchild ); //構造右子樹     }}

注意：

調用該算法時，應將待建立的二叉鍊表的根指針的地址作為實參。

示例

設root是一根指針（即它的類型是BinTree），則調用CreateBinTree(&root）後root就指向了已構造好的二叉鍊表的根結點。

二叉樹建立過程見

下面是關於二叉樹的遍歷、查找、刪除、更新數據的代碼（遞歸算法）：

#include<iostream>#include<cstdio>#include<cmath>#include<iomanip>#include<cstdlib>#include<ctime>#include<algorithm>#include<cstring>#include<string>#include<vector>#include<list>#include<stack>#include<queue>#include<map>#include<set>using namespace std;typedef int T;class bst{    struct Node    {        T data;        Node* L;        Node* R;        Node(const T& d,Node* lp=NULL,Node* rp=NULL):data(d),L(lp),R(rp) {}    };    Node* root;    int num;public:    bst():root(NULL),num(0) {}    void clear(Node* t)    {        if(t==NULL) return;        clear(t->L);        clear(t->R);        delete t;    } ~bst()    {        clear(root);    } void clear()    {        clear(root);        num = 0;        root = NULL;    } bool empty()    {        return root==NULL;    } int size()    {        return num;    } T getRoot()    {        if(empty()) throw "empty tree";        return root->data;    } void travel(Node* tree)    {        if(tree==NULL) return;        travel(tree->L);        cout << tree->data << ' ';        travel(tree->R);    } void travel()    {        travel(root);        cout << endl;    } int height(Node* tree)    {        if(tree==NULL) return 0;        int lh = height(tree->L);        int rh = height(tree->R);        return 1+(lh>rh?lh:rh);    } int height()    {        return height(root);    } void insert(Node*& tree,const T& d)    {        if(tree==NULL)  tree = new Node(d);        else if(ddata)  insert(tree->L,d);        else  insert(tree->R,d);    } void insert(const T& d)    {        insert(root,d);        num++;    } Node*& find(Node*& tree,const T& d)    {        if(tree==NULL) return tree;        if(tree->data==d) return tree;        if(ddata)  return find(tree->L,d);        else  return find(tree->R,d);    } bool find(const T& d)    {        return find(root,d)!=NULL;    } bool erase(const T& d)    {        Node*& pt = find(root,d);        if(pt==NULL) return false;        combine(pt->L,pt->R);        Node* p = pt;        pt = pt->R;        delete p;        num--;        return true;    } void combine(Node* lc,Node*& rc)    {        if(lc==NULL) return;        if(rc==NULL) rc = lc;        else combine(lc,rc->L);    } bool update(const T& od,const T& nd)    {        Node* p = find(root,od);        if(p==NULL) return false;        erase(od);        insert(nd);        return true;    }};int main(){    bst b;    cout << "input some integers:";    for(;;)    {        int n;        cin >> n;        b.insert(n);        if(cin.peek()=='\n') break;    }for(;;)    {        cout << "input data pair:";        int od,nd;        cin >> od >> nd;        if(od==-1&&nd==-1） break;  b.update(od,nd);    }}