基本介紹
- 中文名:不變集
- 外文名:invariant set
- 所屬領域:動力系統
定義
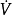
局部不變集定理
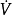
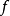
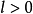
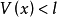
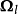
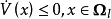
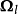
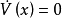

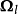
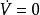

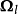
 圖1. 對最大不變集M的收斂
圖1. 對最大不變集M的收斂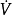
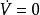
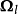


全局不變集定理
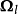
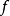
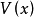
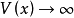
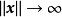
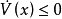

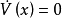


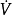
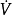
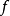
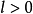
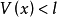
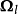
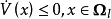
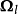
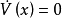

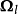
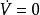

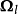
 圖1. 對最大不變集M的收斂
圖1. 對最大不變集M的收斂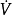
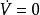
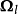


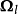
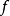
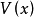
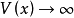
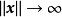
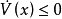

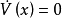

不變集(invariant set)是動力系統中的重要概念之一,是動力系統研究的重要對象。對於自治系統x(k+1)=f(x(k)),如果x(0)∈Ω,有x(k)∈Ω,k=1,2,…,即...
不變集半結構穩定性(structural semi-sta-bility of invariant set)描述動力系統的不變集在系統受到C。...
移位不變集(shift invariant set)在拓撲共輛的意義下能夠等同於符號動力系統(或符號半動力系統)的一種不變集.設M是拓撲空間,.f:M-"M是同胚(或連續自映射.八...
雙曲周期點又稱雙曲不動點,是可微映射具有局部結構穩定性質的不動點。雙曲不變集(hyperbolic invariant set)雙曲周期點概念的推廣,是微分動力系統的一個極為重要...
不變集C結構穩定性(C structural stabilityof invariant set)微分動力系統研究的重要內容之一指系統經過小擾動之後,其不變集不改變其軌道結構,僅僅是不變集各點的...
擴張不變集(expanding invariant set)離散微分半動力系統中較之擴張映射更廣泛的研究對象,是一個重要的不變集.設M是黎曼流形,UCM是具有緊緻閉包的開集,八CU是....
流雙曲不變集(hyperbolic invariant set of aflow)雙曲周期軌概念的推廣,是C'流的一個重要的不變集。...
拉薩爾不變原理是李亞普諾夫第二方法的推廣。這種觀察給出了李亞普諾夫理論的統一認識,且極大地推廣了李亞普諾夫第二方法,現在人們稱這一推廣為拉薩爾不變原理。...
自仿集是一類具有自仿性的集合,對於沿不同方向有不同壓縮係數的線性壓縮族所產生的不變集稱為自仿集。...
極小集(minimal set)是動力系統一個重要的不變集合,設f是M上的一個動力系統,若N是f的非空的閉不變集,並且N中不存在真子集也具有這種性質,則集合N⊂M稱...
鏈回歸集(chain recurrent set) r匕非遊蕩集更廣的一類不變集.設(M,d)是度量空間,f是M到自身的連續映射,{x賺二,是f的一個a偽軌.如果存在整數n>0,使得...
準極小集(quasi-minimal set)具有域回歸性的不變集之一如果一個軌道是泊松式穩定的,並且該軌道的閉包位於緊緻集合中,那么該軌道的閉包稱為是準極小集.準極小...
