不動點組合子

不動點組合子（英語：Fixed-point combinator，或不動點運算元）是計算其他函式的一個不動點的高階函式。

基本介紹

• 中文名：不動點組合子
• 外文名：Fixed-point combinator
• 類別：高階函式
• 定義：非遞歸的lambda 抽象

簡介

不動點組合子（英語：Fixed-point combinator，或不動點運算元）是計算其他函式的一個不動點的高階函式。

函式f的不動點是將函式套用在輸入值 x 時，會傳回與輸出值相同的值，使得f(x) = x。例如，0 和 1 是函式f(x) = x的不動點，因為 0= 0 而 1= 1。鑒於一階函式（在簡單值比如整數上的函式）的不動點是個一階值，高階函式f的不動點是另一個函式g使得f(g) =g。那么，不動點運算元fix的定義是x=f\ x。

使得對於任何函式 f

不動點組合子它們可以用非遞歸的lambda抽象來定義，在 lambda演算中的函式都是匿名的。然而在命令式程式語言中的遞歸，或許限制只能以呼叫函式名稱作為參數來實作。在函式式程式語言中的不動點，以 lambda抽象來定義的Y組合子為：

則允許匿名函式足夠逹成遞歸的作用，即遞歸函式。套用於帶有一個變數的函式，Y組合子通常不會終止。將Y組合子套用於二或更多個變數的函式，會獲得更有趣的結果。第二個變數可當作計數器或索引。由此產生的函式行為，表現出如命令式語言中一個while或for循環。

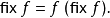
這個組合子也是 Curry悖論的核心，演示了無型別的 lambda演算是一個不穩固的推論系統，因由Y組合子允許一個匿名表達式來表示零或者甚至許多值，這在數理邏輯上是不一致的。

組合子

在無類型lambda演算中眾所周知的（可能是最簡單的）不動點組合子叫做Y組合子。它是Haskell B. Curry發現的，定義為

• Y:= λf.(λx.(f (x x)) λx.(f (x x))) 用一個例子函式g來展開它，我們可以看到上面這個函式是怎么成為一個不動點組合子的：
  
• (Yg)
  
• = (λf.(λx.(f (x x)) λx.(f (x x)))g)
  
• = (λx.(g(x x)) λx.(g(x x)))（λf的β-歸約 - 套用主函式於g）
  
• = (λy.(g(y y)) λx.(g(x x)))（α-轉換 - 重命名約束變數）
  
• = (g(λx.(g(x x)) λx.(g(x x))))（λy的β-歸約 - 套用左側函式於右側函式）
  
• = (g(Yg))（Y的定義）
  

注意Y組合子意圖用於傳名求值策略，因為 (Yg)在傳值設定下會發散（對於任何g）。

存在性

在數學的特定形式化中，比如無類型lambda演算和組合演算中，所有表達式都被當作高階函式。在這些形式化中，不動點組合子的存在性意味著“所有函式都至少有一個不動點”，函式可以有多於一個不同的不動點。

在其他系統中，比如簡單類型lambda演算，不能寫出有良好類型（well-typed）的不動點組合子。在這些系統中對遞歸的任何支持都必須明確的增加到語言中。帶有擴展的遞歸類型的簡單類型lambda演算，可以寫出不動點運算元，“有用的”不動點運算元（它的套用總是會返回）的類型將是有限制的。

例如，在Standard ML中Y組合子的傳值調用變體有類型∀a.∀b.((a→b)→(a→b))→(a→b)，而傳名調用變體有類型∀a.(a→a)→a。傳名調用（正規）變體在套用於傳值調用的語言的時候將永遠循環下去 -- 所有套用Y(f)展開為f(Y(f))。按傳值調用語言的要求，到f的參數將接著展開，生成f(f(Y(f)))。這個過程永遠重複下去（直到系統耗盡記憶體），而不會實際上求值f的主體。

例子

考慮階乘函式（使用邱奇數）。平常的遞歸數學等式

• fact(n) = if n=0 then 1 else n *fact(n-1)
  

可以用lambda演算把這個遞歸的一個“單一步驟”表達為

• F= λf. λx. (ISZERO x) 1 (MULT x (f (PRED x))),
  

這裡的"f"是給階乘函式的占位參數，用於傳遞給自身。 函式F進行求值遞歸公式中的一個單一步驟。 套用fix運算元得到

• fix(F)(n) =F(fix(F))(n)
  
• fix(F)(n) = λx. (ISZERO x) 1 (MULT x (fix(F) (PRED x)))(n)
  
• fix(F)(n) = (ISZERO n) 1 (MULT n (fix(F) (PRED n)))我們可以簡寫fix(F)為fact，得到
  
• fact(n) = (ISZERO n) 1 (MULT n (fact(PRED n)))所以我們見到了不動點運算元確實把我們的非遞歸的“階乘步驟”函式轉換成滿足預期等式的遞歸函式。
  

其他不動點組合子

Y組合子的可以在傳值調用的套用序求值中使用的變體，由普通Y組合子的部分的η-展開給出：

• Z= λf.(λx. f (λy. x x y)) (λx. f (λy. x x y))
  

Y組合子用SKI-演算表達為

• Y= S (K (S I I)) (S (S (K S) K) (K (S I I)))在SK-演算中最簡單的組合子由John Tromp發現，它是
  

• Y'= S S K (S (K (S S (S (S S K)))) K)它對應於lambda表達式
  

• Y'= (λx.λy. x y x) (λy.λx. y (x y x))
  

另一個常見不動點組合子是圖靈不動點組合子（阿蘭·圖靈發現的）:

• Θ= (λx.λy.(y (x x y))) (λx.λy.(y (x x y)))它也有一個簡單的傳值調用形式：
  

• Θ_v= (λx.λy.(y (λz. x x y z))) (λx.λy.(y (λz. x x y z)))
  

參見

• 組合子邏輯
  
• lambda演算
  
• 有類型lambda演算