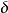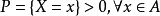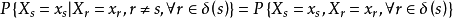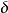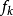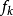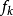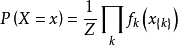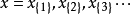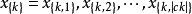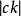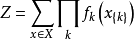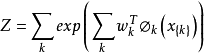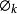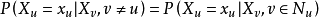馬爾可夫隨機場

馬爾可夫隨機場（Markov Random Field），也有人翻譯為馬爾科夫隨機場，馬爾可夫隨機場是建立在馬爾可夫模型和貝葉斯理論基礎之上的，它包含兩層意思：一是什麼是馬爾可夫，二是什麼是隨機場。

基本介紹

• 中文名：馬爾可夫隨機場
• 外文名：Markov Random Field
• 英文簡稱：MRF
• 性質：數學名詞
• 又稱：馬爾科夫隨機場
• 理論基礎：由馬爾可夫模型和貝葉斯理論奠定
• 套用：建立數學模型

介紹

隨機過程

在當代科學與社會的廣闊天地里，人們都可以看到一種叫作隨機過程的數學模型：從銀河亮度的起伏到星系空間的物質分布、從分子的布朗運動到原子的蛻變過程，從化學反應動力學到電話通訊理論、從謠言的傳播到傳染病的流行、從市場預測到密碼破譯，隨機過程理論及其套用幾乎無所不在。人類歷史上第一個從理論上提出並加以研究的過程模型是馬爾科夫鏈，它是馬爾科夫對機率論乃至人類思想發展作出的又一偉大貢獻。

隨機過程就是描寫敘述某個空間上粒子的隨機運動過程的一種方法。它是一連串隨機事件動態關係的定量描寫敘述。隨機過程與其他數學分支，如微分方程、複變函數等有密切聯繫。是自然科學、project科學及社會科學等領域研究隨機現象的重要工具。

馬爾可夫隨機過程和馬爾可夫鏈

馬爾科夫過程，是指下一個時間點的值只與當前值有關係，與以前沒有關係，即未來決定於現在而不是過去。

用一個通俗的比喻來形容，一隻被切除了大腦的白鼠在若干個洞穴間的躥動就構成一個馬爾可夫鏈。因為這隻白鼠已沒有了記憶，瞬間而生的念頭決定了它從一個洞穴躥到另一個洞穴；當其所在位置確定時，它下一步躥往何處與它以往經過的路徑無關。這一模型的哲學意義是十分明顯的，用前蘇聯數學家辛欽（1894－1959〕的話來說，就是承認客觀世界中有這樣一種現象，其未來由現在決定的程度，使得我們關於過去的知識絲毫不影響這種決定性。這種在已知 “現在”的條件下，“未來”與“過去”彼此獨立的特性就被稱為馬爾科夫性，具有這種性質的隨機過程就叫做馬爾科夫過程，其最原始的模型就是馬爾科夫鏈。

換個說法：馬爾科夫隨機過程是一類隨機過程

馬爾科夫隨機過程是一類隨機過程。它的原始模型馬爾可夫鏈，由俄國數學家A.A.馬爾可夫於1907年提出。該過程具有如下特性：在已知目前狀態 (現在)的條件下，它未來的演變 (將來)不依賴於它以往的演變 ( 過去 ) 。 例如森林中動物頭數的變化構成——馬爾可夫過程。在現實世界中，有很多過程都是馬爾可夫過程，如液體中微粒所作的布朗運動、傳染病受感染的人數、車站的候車人數等，都可視為馬爾可夫過程。關於該過程的研究，1931年A.H.柯爾莫哥洛夫在《機率論的解析方法》一文中首先將微分方程等分析的方法用於這類過程，奠定了馬爾可夫過程的理論基礎。1951年前後，伊藤清建立的隨機微分方程的理論，為馬爾可夫過程的研究開闢了新的道路。1954年前後，W.費勒將半群方法引入馬爾可夫過程的研究。流形上的馬爾可夫過程、馬爾可夫向量場等都是正待深入研究的領域。

人們在實際中常遇到具有下述特性的隨機過程：在已知它目前的狀態(現在)的條件下，它未來的演變（將來）不依賴於它以往的演變（過去）。這種已知“現在”的條件下，“將來”與“過去”獨立的特性稱為馬爾可夫性，具有這種性質的隨機過程叫做馬爾可夫過程。荷花池中一隻青蛙的跳躍是馬爾可夫過程的一個形象化的例子。青蛙依照它瞬間或起的念頭從一片荷葉上跳到另一片荷葉上，因為青蛙是沒有記憶的,當現在所處的位置已知時,它下一步跳往何處和它以往走過的路徑無關。如果將荷葉編號並用X0,X1,X2,…分別表示青蛙最初處的荷葉號碼及第一次、第二次、……跳躍後所處的荷葉號碼，那么{Xn，n≥0} 就是馬爾可夫過程。液體中微粒所作的布朗運動，傳染病受感染的人數，原子核中一自由電子在電子層中的跳躍，人口增長過程等等都可視為馬爾可夫過程。還有些過程（例如某些遺傳過程）在一定條件下可以用馬可夫過程來近似。

馬爾可夫隨機場

馬爾可夫隨機場（Markov Random Field）包含兩層意思。

馬爾可夫性質：它指的是一個隨機變數序列按時間先後關係依次排開的時候，第N+1時刻的分布特性，與N時刻以前的隨機變數的取值無關。拿天氣來打個比方。如果我們假定天氣是馬爾可夫的，其意思就是我們假設今天的天氣僅僅與昨天的天氣存在機率上的關聯，而與前天及前天以前的天氣沒有關係。其它如傳染病和謠言的傳播規律，就是馬爾可夫的。

隨機場：當給每一個位置中按照某種分布隨機賦予相空間的一個值之後，其全體就叫做隨機場。我們不妨拿種地來打個比方。其中有兩個概念：位置（site），相空間（phase space）。“位置”好比是一畝畝農田；“相空間”好比是種的各種莊稼。我們可以給不同的地種上不同的莊稼，這就好比給隨機場的每個“位置”，賦予相空間裡不同的值。所以，俗氣點說，隨機場就是在哪塊地里種什麼莊稼的事情。

馬爾可夫隨機場：馬爾科夫隨機場是具有馬爾科夫特性的隨機拿種地打比方，如果任何一塊地里種的莊稼的種類僅僅與它鄰近的地里種的莊稼的種類有關，與其它地方的莊稼的種類無關，那么這些地里種的莊稼的集合，就是一個馬爾可夫隨機場。

數學描述

馬爾可夫隨機場

在隨機場的基礎上添加馬爾科夫性質，從而得到馬爾科夫隨機場。把馬爾科夫隨機場映射到無向圖中，此無向圖中的節點都與某個隨機變數相關，連線著節點的邊代表與這兩個節點有關的隨機變數之間的關係，所以，馬爾科夫隨機場其實表達出隨機變數之間有些關係因素是必須要考慮的，而另外則有些是可以不用考慮的。馬爾科夫隨機場的某個隨機變數，僅僅只與其相鄰的隨機變數有關，與那些不相鄰的隨機變數無關。
設 為S上的鄰域系統，若隨機場 滿足如下條件：

（1） ;

（2）

則稱X為以 為鄰域系統的馬爾科夫隨機場，上式稱為馬爾科夫隨機場的局部特性。

馬爾可夫隨機場，也叫馬爾可夫網。無向圖模型也叫馬爾科夫隨機場(MarkovRandomFields)或馬爾科夫網路(MarkovNetwork)，無向圖模型有一個簡單的獨立定義：兩個節點集A、B都與給定的第三個節點集C相互條件獨立，A、B節點之間的路徑都被C中的節點分開。

相比之下，有向圖模型也叫貝葉斯網路(Bayesiannetworks)或信念網路(BeliefNetworks)，有向圖模型有一個更複雜的獨立性觀念。

形式上，一個馬爾可夫網路包括：

（1）一個無向圖G= (V,E)，每個頂點v∈V表示一個在集合的隨機變數，每條邊 {u,v} ∈E表示隨機變數u和v之間的一種依賴關係。

（2）一個函式集合 （也稱為因子或者團因子有時也稱為特徵），每一個 的定義域是圖G的團或子團k。每一個 是從可能的特定聯合的指派（到元素k）到非負實數的映射。

聯合分布函式：

聯合分布（吉布斯測度）用馬爾可夫網路可以表示為：

其中 是向量， 是隨機變數 ， 在第k個團的狀態（ 是在第k個團中包含的節點數），乘積包括了圖中的所有團。注意馬爾可夫性質在團內的節點存在，在團之間是不存在依賴關係的。這裡， Z是配分函式，有

實際上，馬爾可夫網聯絡經常表示為對數線性模型。通過引入特徵函式 ，得到

和

以及劃分函式

其中，是權重，是勢函式，映射團k到實數。這些函式有時亦稱為吉布斯勢；術語勢源於物理，通常從字面上理解為在臨近位置產生的勢能。

對數線性模型是對勢能的一種便捷的解釋方式。一個這樣的模型可以簡約的表示很多分布，特別是在領域很大的時候。另一方面，負的似然函式是凸函式也帶來便利。但是即便對數線性的馬爾可夫網路似然函式是凸函式，計算似然函式的梯度仍舊需要模型推理，而這樣的推理通常是難以計算的。

馬爾可夫性質

馬爾可夫網路有這樣的馬爾可夫性質：圖的頂點u在狀態的機率只依賴頂點u的最近臨節點，並且頂點u對圖中的其他任何節點是條件獨立的。該性質表示為

頂點u的最近臨節點集合也稱為頂點u的馬爾可夫毯。

特點

馬爾科夫隨機場具有以下幾個鮮明的特點：
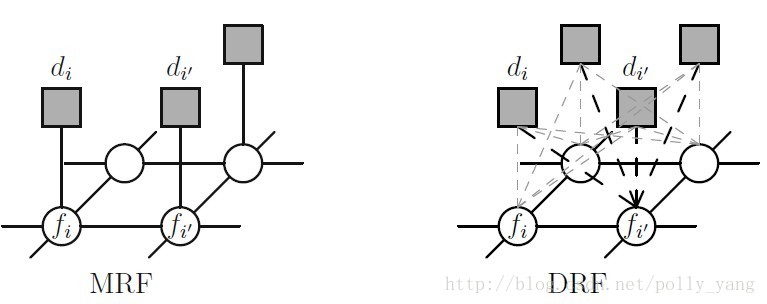
（1）馬爾科夫模型中，像素的空間關係可以傳播，通過像素之間的相互作用，從而低階馬爾科夫隨機場可以被用來描述的像素之間的關係；
（2）在馬爾科夫隨機場模型不僅可以表示出的圖像的隨機性，同時又能表示出圖像的底層結構，因此道路場景的性質能夠被很好的表述；
（3）馬爾科夫隨機場模型，從物理模型出發，同時也直接關係到道路場景圖像的數據（灰色值或特徵）；
（4）Besag對MRF的深入研究，得出吉布斯分布於馬爾科夫隨機場的關係，使得馬爾科夫隨機場與能量函式相關在一起；
（5）求解馬爾科夫隨機場描述的不確定性問題，利用統計決策、估計理論、貝葉斯理論，將道路場景的先驗知識用先驗分布模型表示，使用最大後驗估計作為道路場景分割的標準。