基本介紹
遞歸論簡介,經典遞歸論,廣義遞歸論,套用,
遞歸論簡介
遞歸論亦稱可計算性理論(computability theory)，數理邏輯分支之一。它是研究關於可計算性與可定義性的數學理論，主要關注於事物的可計算性，可定義性及其分層。遞歸論起源於20 世紀30 年哥德爾、丘奇、圖靈、克林和波斯特(E.Post) 等關於自然數集合的可計算性的研究。
經典遞歸論
經典的遞歸論關注於自然數集合的可計算性。絕大多數自然數集合都是不可計算的。對於不可計算的集合，可以加以複雜性比較。例如圖靈歸約就是一種典型的比較方式。這些比較可以看作一種廣義上的分層。遞歸論關注於這些比較方式及其產生的代數結構。對於這些比較方式產生的代數結構的研究已經形成門被稱為度論的比較成熟的領城。這些度結構中以圖靈度的研究最為廣泛。它們的研究起源於克林和波斯特。
對於一般圖靈度的結構的研究，早期經過克林、弗賴德貝格(R.M.Fiedberg)、斯佩克特(C Spector)、薩克斯(G.Sacks)、休恩菲爾德、耶茨(C.E M.Yates)、庫珀(S.B.Coper) 等的長期積累，證明了大量的關於圖靈度的局部性質並且引入了許多構造圖靈度的方法。
20 世紀80年代開始圖靈度的結構研究開始轉向大範圍結構的研究，即更加關注於圖靈度結構的模型論性質及其理論的可判定性。
關於圖靈度結構理論的可判定性，1977 年辛普森(S.Simpson) 證明了圖靈度的結構理論與二階算術是遞歸同構的，從而刻畫了圖靈度結構理論的複雜性。
對於圖靈度結構理論的片段，克林和波斯特事實上已經證明了圖靈度的
理論是可判定的。
施梅爾(J.Schmerl) 證明了圖靈度的
理論是不可判定的。萊爾曼(M.Lerman) 和肖爾(R.Shore) 最終證明了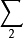
理論是不可判定的。
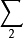
關於圖靈度結構的模型論性質有兩個非常重要也非常困難的問題。第一個問題: 圖靈躍變是否在一般圖靈度結構中可定義? 第二個問題: 是否存在圖靈度的非平凡自同構? 有不少人曾致力於解決這些問題。最後，第一個問題由思萊曼(T.Slaman) 和肖爾於1999 年在思萊曼和武丁工作的基礎上用完全不同於以前的方法肯定地解決。而迄今為止，第二個問題依然懸而未決。最近的進展是思萊曼和武丁證明了圖靈度結構的自同構群至多可數。
遞歸可枚舉的圖靈度的結構問題也是這一領域廣受關注的課題之一。它起源於波斯特關於是否存在嚴格介於遞歸集和停機問題（即圖靈躍變） 的遞歸可枚舉圖靈度的問題。
這一問題被穆奇尼克(A.Muchnik) 和弗賴德貝格分別給予了肯定的答案。他們引入的現在被稱為有窮損害的方法已經成為這一領域的基本工具之一。後來休恩菲爾德、薩克斯、拉克倫(A.Lachlan) 分別引入了無窮損害以及所謂的0'''優先方法，這些方法現在已經成為強有力的構造遞歸可枚舉圖靈度的工具。
20 世紀80 年代開始研究開始轉向遞歸可枚舉圖靈度的模型論結構理論。
可判定性方面，1982 年哈林頓和謝拉赫證明了遞歸可枚舉圖靈度結構的理論是不可判定的。
薩克斯證明了遞歸可枚舉圖靈度的理論是可判定的。蘭普(S.Lempp)、尼斯(A.Nies) 和思萊曼證明了遞歸可枚舉圖靈度的理論是不可判定的。關於遞歸可枚舉圖靈度的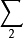理論是否可判定仍然未知。
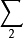
哈林頓和思萊曼，思萊曼和武丁，尼斯和肖爾以及思萊曼先後用不同的編碼方法證明了遞歸可枚舉圖靈度的理論與一階算術理論是遞歸同構的，因此刻畫了遞歸可枚舉圖靈度理論的複雜性。模型論方面，尼斯、肖爾和思萊曼證明了遞歸可枚舉度中許多類是可定義的。但遞歸可枚舉度低度是否在遞歸可枚舉圖靈度中可定義仍然未知。
廣義遞歸論
廣義的遞歸論研究一般數學事物的可計算性和可定義性。一般有兩種方式推廣經典的遞歸論。一種是把圖靈機加以推廣。例如，把圖靈機推廣到實數上就能研究實數集合的可計算性，把圖靈機推廣到序數上，就能研究序數集合的可計算性。魏勞赫(K.Weihrauch) 提出的實數上的圖靈機以及布盧姆(L Blum).舒布(M.Shub) 和斯梅爾(S.Smale) 提出的BSS 機器都是這一方向比較流行的理論。另外一種推廣方式是研究可定義性。可定義性本身可以看作可計算性的推廣。因此遞歸論學家可以運用經典的遞歸論工具研究一類特定的可定義集合的性質。這一方向往往與集合論相交叉。例如，博雷爾集就是超算術實數集的“相對化”，可構成集合可以看成一種廣義的遞歸的集合等。
套用
近來遞歸論更多地關注於它對其他學科的套用。例如，遞歸模型論、反推數學、算法隨機性理論都是現在廣泛關注的領城，遞歸論在這些領城中都有成功的套用。
