基本介紹
- 中文名:無窮性公理
- 含義:集合論中肯定無窮集合存在的公理
- 建立者:G.F.P.康托爾
- 相關概念:大基數公理
- 套用學科:集合論
- 本質:有一個集合包含所有的自然數
建立過程,形式陳述,解釋,
建立過程
G.F.P.康托爾在建立集合論時,發現僅靠邏輯公理不能保證有無窮集合存在,因為沒有一個一階公式能在無窮個體域有效而在有窮個體域上不有效。而利用ZF系統中的公理①~⑥及⑧、⑨(見集合論)雖然可以定義一個個具體的自然數,也可以定義自然數概念,但卻無法證明全體自然數的集合w={0,1,… }存在,也無法證明任何一個無窮集合的存在性。實際上,如果ZF(有模型,則全體繼承性有窮的集合,即其本身有窮、其元素有窮、其元素的元素有窮……仍是ZF(的模型。即便如此,ZF(公理仍不能保證無窮集的存在,而必須有一條專門的公理。
按照無窮性公理,最基本的無窮集是自然數集w,w的最突出的特點是歸納性它表現為如果 ∈,並且∈A^0蘊涵wU∈A,就稱A為歸納集。無窮公理通常就是從這個角度陳述的。利用無窮性公理和子集公理(見子集公理模式)可以定義w為最小的歸納集,一旦有了w就可以證明歸納原則和遞歸定理,然後就可以遞歸地定義自然數上的各種運算。例如, 可以把加法定義為m+0=m,n+s(n)=s(m+n);乘法定義為m·0=0,m·s(n)=m·n+m。例中m為任意自然數,自然數之間的<關係定義為∈。容易驗證,這樣定義出的自然數與直觀的自然數概念是吻合的。利用w和ZF公理可以定義整數、有理數、實數、複數等各種數學對象及其運算,也可以推出形形色色的無窮集合的存在性。
現代集合論中還有一些強無窮性公理,也叫大基數公理,它們斷言有各種大基數存在,現已提出的大基數達數十種,它們都可以看作是w的某種推廣。
形式陳述
在 Zermelo-Fraenkel 公理的形式語言中,這個公理讀作:

或用非形式化的語言陳述:存在一個集合N,使得空集在N中,並且只要x是N的成員,則x與它的單元素集合{x} 此兩者的並集也是N的成員。這種集合有時也叫做歸納集合。歸納集合是帶有如下性質的集合X:對於所有x ∈ X,x的後繼x' 也是X的一個元素。
解釋
要理解這個公理,首先我們要定義x的後繼為x∪ {x}。注意配對公理允許我們形成單元素集合 {x}。 後繼是用來定義自然數的常用的集合論編碼。在這種編碼中,0是空集(0 = {}),而1是 0 的後繼:
- 1 = 0 ∪{0} = {} ∪ {0}= {0}
類似地,2 是1 的後繼:
- 2 = 1 ∪ {1} = {0} ∪ {1} = {0,1}
如此類推。這個定義的推論是對於任何自然數n,n等同於由它的所有前驅(predecessor)組成的集合。
我們希望可以形成包含所有自然數的一個集合,但是只使用其他ZF公理的話並不能做到這一點。因此,有必要加入無窮公理以假定這個集合的存在。它是通過類似於數學歸納法的方法完成的:首先假定有一個集合S包含零,並接著規定對於S的所有元素,這個元素的後繼也在S中。
這個集合S可以不只是包含自然數,還包含別的元素。但是我們可以套用分類公理模式來除去不想要的元素,留下所有自然數的集合N。通過外延公理可知這個集合是唯一的。套用分類(分離)公理的結果是:

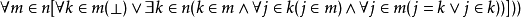
用非形式化的語言陳述:所有自然數的集合存在;這裡的自然數要么是零,要么是一個自然數k的後繼,並且k的每個元素要么是0要么是k的另外一個元素的後繼。
所以這個公理的本質是:
- 有一個集合包含所有的自然數。
無窮公理也是von Neumann-Bernays-Gödel 公理之一。

