基本介紹
- 中文名:歐拉線
- 外文名:Euler Line
- 定理內容:三角形的重心、垂心和外心共線
定義,證法,證法1,證法2,證法3,套用,
定義
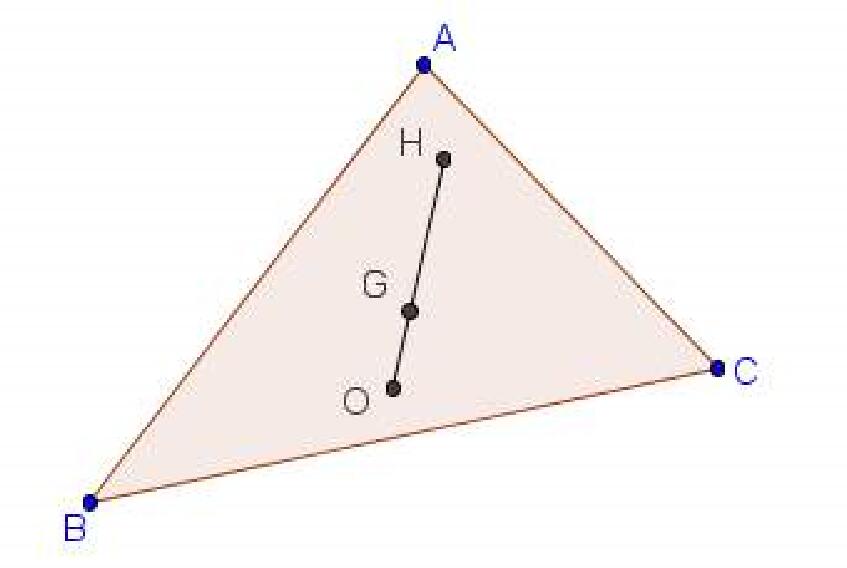
如右圖,歐拉線(圖中的紅線)是指過三角形的垂心(藍)、外心(綠)、重心(黃)和歐拉圓圓心(紅點)的一條直線。 歐拉線
歐拉線
 歐拉線
歐拉線證法
證法1
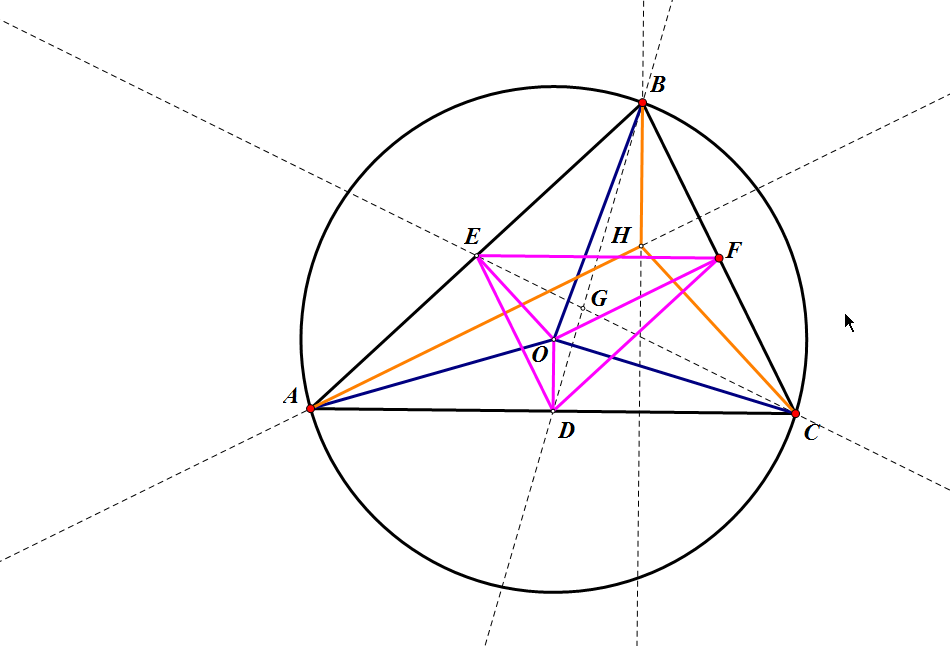
設H,G,O,分別為△ABC的垂心、重心、外心。聯結AG並延長交BC於D, 則可知D為BC中點。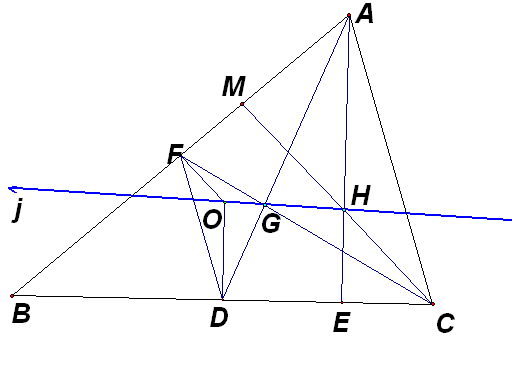

聯結OD ,又因為O為外心,所以OD⊥BC。聯結AH並延長交BC於E,因H為垂心,所以 AE⊥BC。所以OD//AE,有∠ODA=∠EAD。由於G為重心,則GA:GD=2:1。
聯結CG並延長交BA於F,則可知F為AB中點。同理,OF//CM.所以有∠OFC=∠MCF
聯結FD,有FD平行AC,且有DF:AC=1:2。FD平行AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相減可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HCA,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以HA:OD=GA:GD=2:1
又∠ODA=∠EAD,所以△OGD∽△HGA。所以∠OGD=∠AGH,又聯結AG並延長,所以∠AGH+∠DGH=180°,所以∠OGD+∠DGH=180°。即O、G、H三點共線。
證法2
還是向量做法,
∵OD⊥AC
∴OD⊥EF
同理OE⊥DF,OF⊥DE
∴O是△DEF的垂心。
又EF∥AC,DF∥AB,DE∥BC且△ABC∽△DEF
∴向量HB=-2向量OD,向量HA=-2向量OF,向量HC=-2向量OE
∴向量HA+向量HB+向量HC=-2向量OD-2向量OE-2向量OF=-2向量OA-2向量OB-2向量OC
又向量BG=2/3向量BD=1/3(向量BA+向量BC)
同理向量CG=1/3(向量CA+向量CB),向量AG=1/3(向量AB+向量AC)
∴向量BG+向量AG+向量CG=向量0
向量HG=向量HA+向量AG=向量HB+向量BG=向量HC+向量CG
向量OG=向量OA+向量AG=向量OB+向量BG=向量OC+向量CG
∴3向量HG=向量HA+向量HB+向量HC,3向量OG=向量OA+向量OB+向量OC
∴向量HG=-2向量OG
證法3
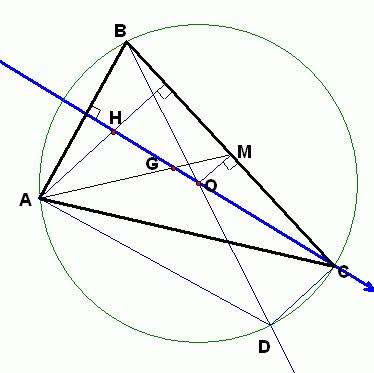
如圖所示,設AM為△ABC的中線,H、O分別是垂心和外心,連線AH、OM,則OM⊥BC,AH⊥BC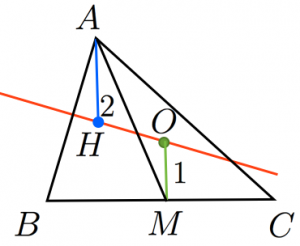

∴AH∥OM
連線OB、OC,易證∠BAC=∠BOC/2=∠COM
∴OM=OCcos∠COM=Rcos∠BAC(R是△ABC外接圓半徑)
又連線BH並延長交AC於D,則BD⊥AC
∴AH=AD/cos∠CAH=ABcos∠BAC/sin∠ACB=2Rcos∠BAC
∴AH=2OM
設OH和AM交於G,則△AHG∽△MOG
∴AG:GM=AH:OM=2:1
∴G是△ABC的重心,即O、H、G三點共線,且GH:GO=AG:GM=2:1
套用
1 : 平面上共圓的5個點,任取其中3點組成三角形,過其重心作另外兩點連線的垂線,共有10條。則這10線交於一點。
證明:設5個點對應的向量分別是z1, z2, z3, z4, z5,且它們的模相等。
因為|z1|=|z2|,所以0, z1, z2, z1+z2這四個點構成一個菱形,所以它們的對角線垂直,所以垂直於z1、z2的連線就相當於平行於z1+z2。
這樣經過三角形z3, z4, z5的重心,且垂直於z1, z2連線的直線方程就是
z(t) = (z3+z4+z5)/3 + t(z1+z2),其中t是任意實數。
取 t=1/3,就得到(z1+z2+z3+z4+z5)/3在這直線上。同理可得這點在所有這類直線上。
3:平面上共圓的5個點,任取其中3點組成三角形,過其九點圓圓心作另外兩點連線的垂線,共有10條。則這10線交於一點。
證明:第2,3個結論緣於以下事實:歐拉線上的四點中,九點圓圓心到垂心和外心的距離相等,而且重心到外心的距離是重心到垂心距離的一半。