基本介紹
算法流程,複雜度分析,
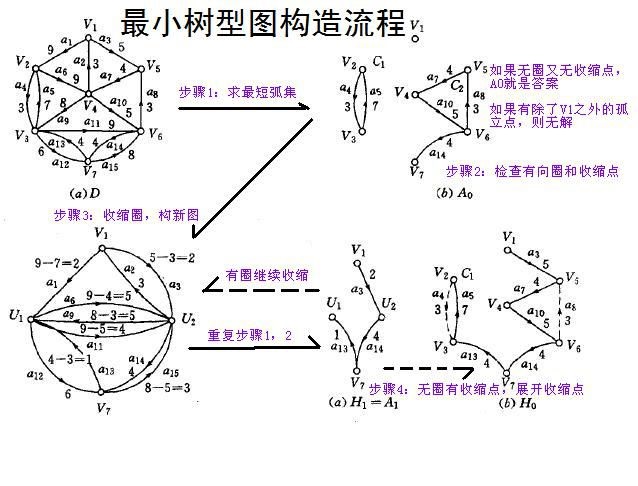
算法流程
判斷是否存在樹形圖的方法很簡單,只需要以v為根作一次圖的遍歷就可以了,所以下面的算法中不再考慮樹形圖不存在的情況。
在所有操作開始之前,我們需要把圖中所有的自環全都清除。很明顯,自環是不可能在任何一個樹形圖上的。只有進行了這步操作,總算法複雜度才真正能保證是O(VE)。
首先為除根之外的每個點選定一條入邊,這條入邊一定要是所有入邊中最小的。所有的最小入邊都選擇出來了,如果這個入邊集不存在有向環的話,我們可以證明這個集合就是該圖的最小樹形圖。這個證明並不是很難。如果存在有向環的話,我們就要將這個有向環縮成一個人工頂點,同時改變圖中邊的權。假設某點u在該環上,並設這個環中指向u的邊權是in[u],那么對於每條從u出發的邊(u, i, w),在新圖中連線(new, i, w)的邊,其中new為新加的人工頂點; 對於每條進入u的邊(i, u, w),在新圖中建立邊(i, new, w-in[u])的邊。為什麼入邊的權要減去in[u],這個後面會解釋,在這裡先給出算法的步驟。然後可以證明,新圖中最小樹形圖的權加上舊圖中被收縮的那個環的權和,就是原圖中最小樹形圖的權。
上面結論也不做證明了。依據上面的結論,說明一下為什麼出邊的權不變,入邊的權要減去in [u]。對於新圖中的最小樹形圖T,設指向人工節點的邊為e。將人工節點展開以後,e指向了一個環。假設原先e是指向u的,這個時候我們將環上指向u的邊 in[u]刪除,這樣就得到了原圖中的一個樹形圖。我們會發現,如果新圖中e的權w'(e)是原圖中e的權w(e)減去in[u]權的話,那么在我們刪除掉in[u],並且將e恢復為原圖狀態的時候,這個樹形圖的權仍然是新圖樹形圖的權加環的權,而這個權值正是最小樹形圖的權值。所以在展開節點之後,我們得到的仍然是最小樹形圖。逐步展開所有的人工節點,就會得到初始圖的最小樹形圖了。
複雜度分析
如果實現得很聰明的話,可以達到找最小入邊O(E),找環 O(V),收縮O(E),其中在找環O(V)這裡需要一點技巧。這樣每次收縮的複雜度是O(E),然後最多會收縮幾次呢?由於我們一開始已經拿掉了所有的自環,我門可以知道每個環至少包含2個點,收縮成1個點之後,總點數減少了至少1。當整個圖收縮到只有1個點的時候,最小樹形圖就不用求了。所以我們最多只會進行V-1次的收縮,所以總得複雜度自然是O(VE)了。由此可見,如果一開始不除去自環的話,理論複雜度會和自環的數目有關。
1986年, Gabow, Galil, Spencer和Tarjan提出了一個複雜度更好的實現,其時間複雜度為O(E+VlogV)。