基本介紹
- 中文名:拉格朗日中值定理
- 外文名:Lagrange Mean Value Theorem
- 別稱:有限增量定理
- 表達式:f(b)-f(a)=f'(ξ)(b-a)(a<ξ<b)
- 提出者:拉格朗日
- 提出時間:1797年
- 套用學科:高等數學
- 適用領域範圍:微分學
- 適用領域範圍:高等數學
定律定義
定理表述
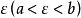

其他形式
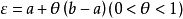
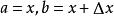
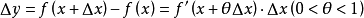
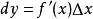
驗證推導

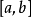
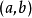
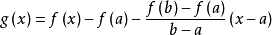
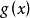
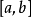
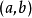

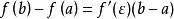
定理推廣
推論
證明
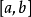

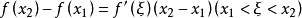
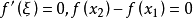
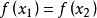
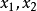
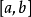
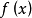
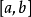
推廣
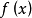
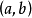
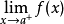
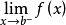

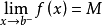
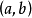
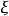
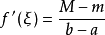
有限增量公式的θ

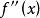
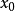

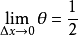
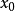
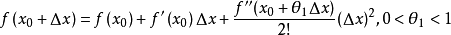
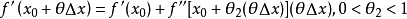
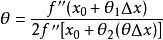
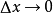
導函式連續定理
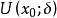
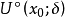
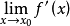
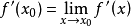
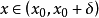
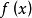
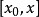
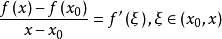
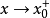
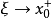

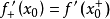
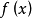
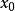
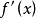
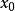
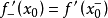
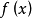
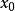
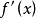
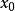
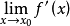
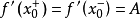

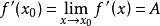
發展簡史
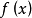

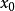


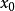
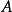
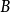
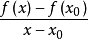
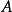
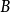
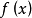
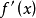


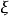
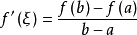

意義
幾何意義
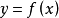
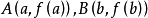
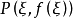
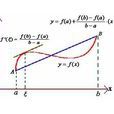
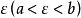

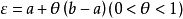
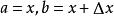
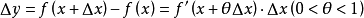
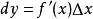

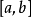
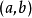
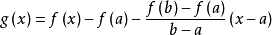
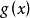
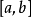
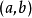

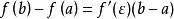
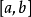

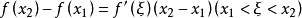
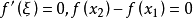
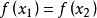
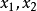
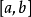
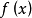
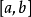
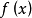
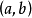
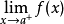
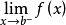

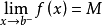
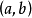
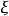
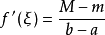

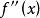
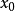

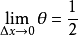
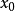
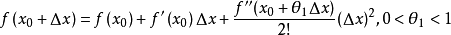
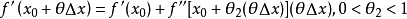
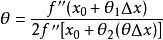
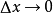
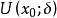
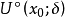
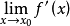
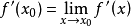
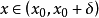
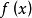
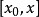
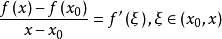
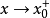
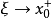

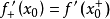
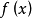
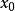
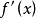
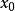
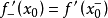
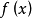
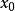
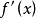
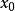
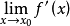
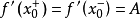

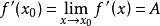
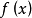

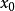


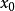
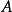
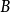
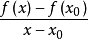
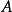
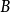
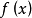
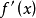


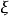
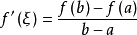

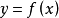
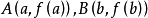
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
拉格朗日定理存在於多個學科領域中,分別為:微積分中的拉格朗日中值定理;數論中的四平方和定理;群論中的拉格朗日定理 (群論)。...
中值定理是反映函式與導數之間聯繫的重要定理,也是微積分學的理論基礎,在許多方面它都有重要的作用,在進行一些公式推導與定理證明中都有很多套用。中值定理是由眾多...
《拉格朗日中值定理:從一道北京高考試題的解法談起》是2015年出版的圖書,作者是佩捷。...
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
拉格朗日就在《解析函式論……》中,第一次得到微分中值定理(書中第六章)f(b)-f(a)=f′(c)(b-a)(a≤c≤b),(12)後面並用它推導出泰勒(Taylor)級數,...
例如用來證明單調有界定理,閉區間上的連續函式的性質(有界性、最值性、零點存在性、一致連續性等),拉格朗日中值定理等微分學上常用的定理。作為介紹,在這裡給出...
著名的拉格朗日中值定理、拉格朗日餘項、拉格朗日方程,對黎卡提方程的重要研究,對線性微分方程組的研究,對奇解與通解的聯繫的系統研究,都是這一時期的工作。他也是...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...拉格朗日定理 (群論)拉格朗日中值定理拉姆齊定理拉克斯-米爾格拉姆定理...
k階中值定理是微分中值定理的推廣。...... 微分中值定理是一系列中值定理總稱,是研究函式的有力工具,其中最重要的內容是拉格朗日定理,可以說其他中值定理都是...
我們知道,根據拉格朗日中值定理導出的有限增量定理有:於是:其中誤差α是在Δx→0即x→x0的前提下才趨向於0,所以在近似計算中往往不夠精確。於是我們需要一個能夠...
根據拉格朗日中值定理。必存在x1<μ< ax1+(1-a)x2;使f[ax1+(1-a)x2]-f(x1)= (1-a)(x2-x1)f'(μ);同理。存在ax1+(1-a)x2<ξ<x2;...
在區間 上對函式 套用拉格朗日中值定理得其中 因此有證畢。 [3] 牛頓-萊布尼茨公式定理推廣 編輯 牛頓-萊布尼茨公式二重積分形式 設函式 在矩形區域 上連續,如果...
1.1 用導數定義求極限1.2 用拉格朗日中值定理求極限1.3 用等價無窮小代換求極限1.4 用泰勒公式求極限1.5 施篤茲定理及其套用1.6 廣義洛必達法則及其套用...
5. 理解並會用羅爾(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解並會用柯西( Cauchy )中值定理.6. 掌握用洛必達法則求未定式極限的方法....
+α(根據拉格朗日中值定理導出的有限增量定理有limΔx→0 f(x.+Δx)-f(x.)=f'(x.)Δx),其中誤差α是在limΔx→0 即limx→x.的前提下才趨向於...
4.4拉格朗日中值定理684.5伽利略的困惑694.6泰勒展開704.7泰勒其人其事73第5章股市的預測795.1證券交易市場的起起落落805.2曲線的擬合805.3再探函式81...
2.6 羅爾定理.拉格朗日定理和柯西定理(習題1235-1267)2.6.1 羅爾定理(習題1235-1243)2.6.2 拉格朗日中值定理(習題1244-1251)...
