基本介紹
- 中文名:可逆線性變換
- 外文名:invertible linear transformation
- 別稱:非退化線性變換,滿秩線性變換
- 所屬學科:數學
- 所屬問題:高等代數(線性變換)
可逆線性變換的定義


相關性質及證明





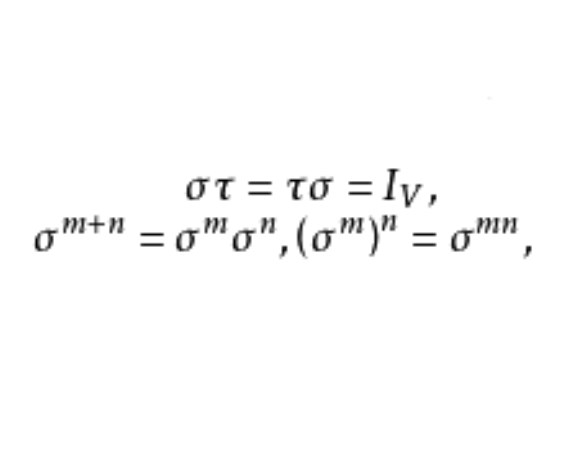







可逆線性變換(invertible linear transformation)亦稱非退化線性變換,或滿秩線性變換,是一種特殊的線性變換,設V是數域P上的線性空間,σ是V的線性變換,若存在V的...
可逆線性變換亦稱非退化線性變換,或滿秩線性變換,是一種特殊的線性變換。設V 是數域 P 上的線性空間,σ是 V 的線性變換。若存在 V 的變換 τ ,使στ=τ...
對合變換(involutory transformation)是一種特殊的冪麼變換。冪麼變換是一種特殊的可逆線性變換。可逆線性變換亦稱非退化線性變換,或滿秩線性變換。一種特殊的線性...
冪麼變換是一種特殊的可逆線性變換。設V是數域P上的線性空間,σ是V的線性變換。若存在自然數m,使σm=l,σm-1≠l,l為單位變換,則a稱為冪麼變換,m稱為...
非奇異線性變換(nonsingular linear transfor-mation)是一類重要的線性變換。設V是域P上的線性空間,σ∈HomP(V,V),若存在λ∈HomP(V,V),使λσ=E(單位...
線性變換多項式是一種特殊的線性變換。線性變換是線性代數研究的一個對象,即向量空間到自身的保運算的映射,線性變換的冪滿足指數法則。...
一般線性群亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為...
線性李群(linear Lie group)一種重要的李群.由可逆線性變換構成的李群.設F為實數域或複數域。...
在數學中,一般線性群是指基域K上n×n 可逆矩陣全體組成的矩陣乘法群。在任何域 F或環 R上的 n 次一般線性群是帶有來自 F(或 R)的元素的 n×n 可逆矩陣...
一般線性群亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為...
(5)慣性定理 對於任意一個n元實二次型f=x'Ax,必存在可逆線性變換x=Rz,這裡R是n階可逆矩陣,把它化為規範形f( )=x'Ax=其中k和r是由A唯一確定的(與所...
過渡矩陣是基與基之間的一個可逆線性變換,在一個空間V下可能存在不同的基。假設有2組基分別為A,B。由基A到基B可以表示為B=AP,過渡矩陣P=A^-1B。它表示...
設G是有限群,V是複數域 C上的有限維向量空間,GL(V)是V上全體可逆線性變換所組成的群。從G 映入GL(V)的一個同態(見公式1 )稱為G的一個表示,而V稱為ρ...
亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為GL(V).體...
合痕(isotopy)是代數學的基本概念,指兩個非結合代數之間的三個可逆線性變換滿足的一種特殊的保乘關係。設(A,+,·)和(A′,#,*)都是域F上的非結合代數,f...
和有失真壓縮的小波變換和以此為基礎的基於感興趣區域的圖像壓縮;承擔國家973課題“信息安全、傳輸與可靠性研究”期間,建立了一般可逆線性變換可整數實現的理論,給出...
記A為n階實非奇異方陣,Rn上線性變換σ:y=Ax稱為關於V不變,如果σ(V)=V,所有使V不變的可逆線性變換構成的集合,記為Aff(V)。...
5.3.2 用可逆線性變換化二次型為標準形5.3.3 矩陣契約的判定與求法5.3.4 求具體矩陣的特徵值與特徵向量5.3.5 求抽象矩陣的特徵值...
GLk(R)在Fx上這個作用是自由傳遞的(這是標準線性代數結論:存在惟一可逆線性變換將一個基變為另一個)。作為一個拓撲空間Fx同胚於GLk(R),但它沒有群結構,因為...
並使G為其李變換群.對於gEG,xEM,則F、二一g-1 f'}}g,且G在GlFs,GlF二二上的作用是等價的.對於gEF=,dg是切空間T=M的可逆線性變換,且d<g,gZ>=dg,...
