基本介紹
一、定義
1. 下界

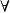

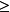
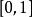


2. 下確界

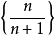
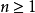
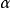

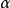

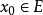
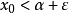
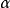


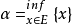
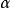
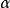
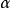
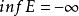
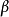

二、常用結論
1. 確界的唯一性定理
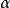

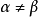
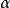



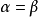
2. 確界存在定理
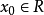


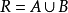
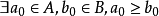
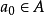
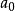
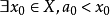
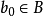
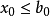
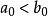
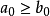
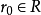
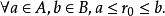
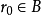
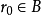
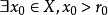
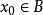
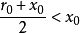
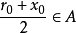
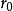
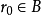
3. 單調有界數列必有極限
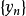
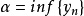
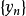
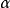
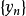
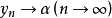
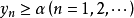
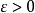
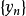
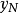
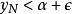
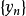


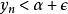

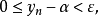
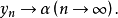



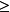
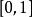



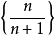
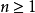
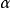

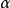

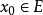
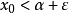
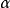


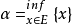
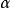
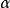
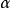
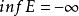


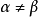
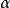



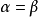
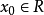


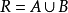
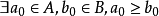
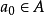
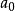
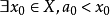
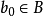
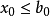
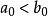
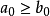
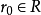
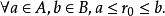
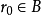
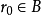
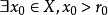
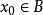
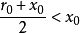
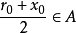
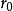
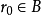
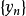
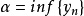
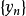
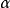
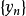
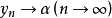
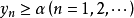
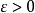
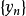
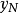
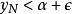
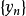


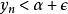

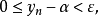
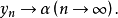
“下確界”是數學分析中的基本概念,它是在“下界”的基礎上定義的。任給一數集E,我們稱E的最大下界為E的下確界,記為infE. 顯然,E中每個元素均大於或等於...
上確界是一個集合的最小上界。下確界是與上確界相對偶的概念,指的是一個集合的最大下界。...
確界原理( supremum and infimum principle )是刻畫實數完備性的命題之一。設S為非空數集。若S有上界,則S必有上確界;若S有下界,則S必有下確界。...
若數集S為實數集R的子集有上界,則顯然它有無窮多個上界,而其中最小的一個上界常常具有重要的作用,稱它為數集S的上確界。[1] ...
5.8正多邊形等積分割線下確界的又幾個結果180第6章點集構造與離散計數1916.1祖點集的一種構造方法1916.2Z圖形的存在性與點集距離的幾個定理193...
正式地,對狀態空間中的某個狀態,馬爾可夫鏈對一給定狀態的返回時間(return time)是其所有可能返回時間的下確界(infimum) [1] :...
(ii)對∀a<η,存在x0∈S,使得x0>a,即η是S的最小上界(least upper bound),則稱η為數集S的上確界;下確界定義:設S是R的一個數集,若數ξ∈S滿足...
下包絡原理是描述兩個位勢的下確界仍是位勢的一個原理。所有的α核都滿足下包絡原理。...
下極限函式是為判斷函式下半連續性而引進的一個概念。設f(x)是定義在點集E上的擴充實值函式,若在閉包E內的點x的δ鄰域與E的交內,函式f所取的值的下確界...
給定無窮序列,由它的一切收斂子序列的極限值所成之集合中元素的下確界,稱為該無窮序列的下極限。...
最優子空間是實現整體偏差最小的子空間。最優子空間的表達式中右邊的下確界是對X的全部n維子空間取的。...
弱哈納克不等式(weak Harnack inequality)有界可測係數的散度形式的橢圓型方程的非負上解在一個球上的下確界控制它在同心倍球上的1r範數的不等式.設散度形式二...
波萊爾函式經過有限次的加、減、乘、除運算以及函式的複合,仍然是波萊爾函式;波萊爾函式列的(上、下)極限以及上確界和下確界仍然是波萊爾函式。...
如果x的關於A的一切下界有一最大元α0,就稱α0為x(關於A)的下確界,記為infx。仿此可定義上界和上確界,後者記為supx。A上的偏序≤,如果再加上條件④...
交運算(meet)即在格中求兩個元素的下確界的過程。 在布爾代數中,交運算相當於邏輯與運算。在集合論中,交運算相當於交集或並集運算。 ∧定義變換函式 編輯 比...
,則稱z是x和y的最小上界,也稱為上確界或上端,記為sup(x,y)或 。類似地可以定義x和y的下界,下確界(下端),記為inf(x, y)或 。如果半序線性空間E中任...
令等於,其中和是在上的上確界和下確界。再令是和中的較小者。可以看出,當一個分割的子區間長度最大值小於時,關於它的黎曼和與上達布和或下達布和至多相差,...
格的定義:設(L,≤)是偏序集,若L中任意兩個元素都存在上確界以及下確界,則稱(L,≤)是格(lattice),為了方便,這樣的格成為偏序格。...
“格”一種特殊的偏序集。在許多數學對象中,所考慮的元素之間具有某種順序。在數學中,完全格是在其中所有子集都有上確界(並)和下確界(交)的偏序集。完全格...
設<A,≤,>為有序集,B是A的子集,則有如下相關定義:B的最小元、最大元、極大元、極小元、上界、下界、上確界、下確界及A的鏈、反鏈。對於有序集上各...
作為柯西收斂準則的套用之一,我們可以用來證明實數的確界原理。確界原理:非空有上(下)界數集,必有上(下)確界。證明:先證非空有上界數集必有上確界。...
